numpy.linalg.LinAlgError: Singular matrix [Solved]

# Table of Contents

# numpy.linalg.LinAlgError: Singular matrix [Solved]

The error "numpy.linalg.LinAlgError: Singular matrix" occurs when you try to invert a singular matrix that has a determinant of 0.

To solve the error, make sure the matrix you are inverting has a matrix inverse and is not singular or use the np.linalg.pinv() method.

Here is an example of how the error occurs.

main.py

Copied!
import numpy as np

arr = np.array([
    [2, 4],
    [2, 4],
])

# ⛔️ numpy.linalg.LinAlgError: Singular matrix
print(np.linalg.inv(arr))

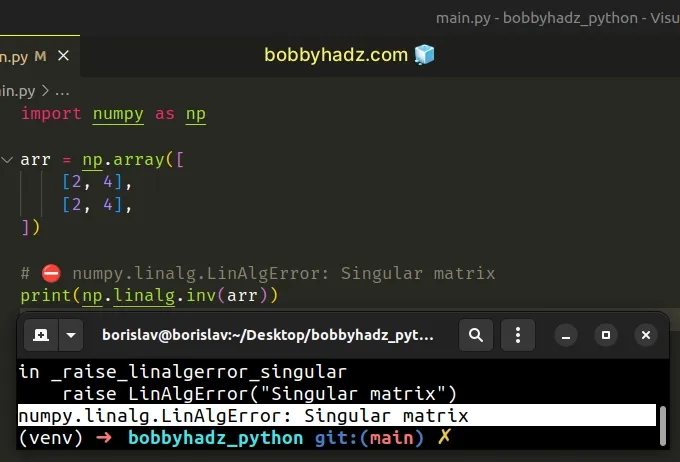
numpy linalg linalgerror singular matrix

We got the error because we tried to invert a singular matrix.

A singular matrix is a square matrix that doesn't have a matrix inverse.

The determinant of a singular matrix is 0, so it can't be inverted.

# Make sure the matrix is invertible

One way to solve the error is to make sure that the matrix is invertible.

main.py

Copied!
import numpy as np

arr = np.array([
    [1, 2],
    [3, 4]
])


# [[-2.   1. ]
#  [ 1.5 -0.5]]
print(np.linalg.inv(arr))

print('-' * 50)

# -2.0000000000000004
print(np.linalg.det(arr))

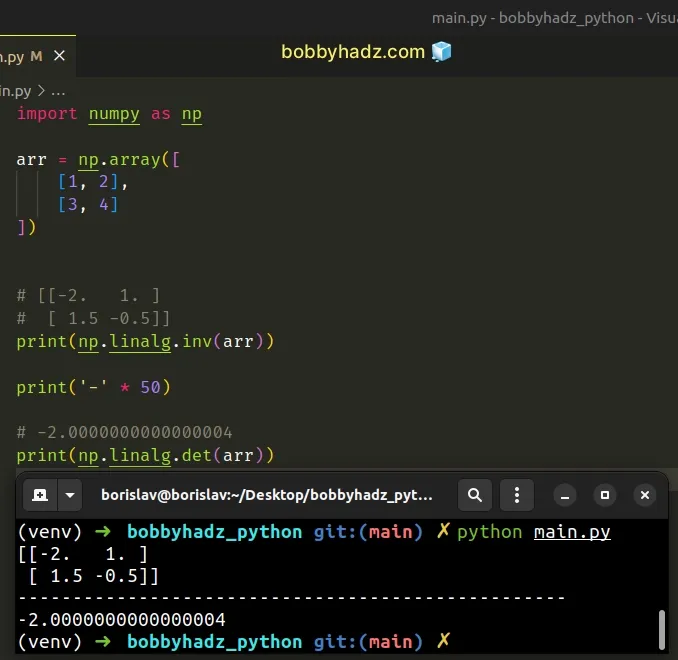
make sure matrix is invertible

The code for this article is available on GitHub

The numpy.linalg.inv() method computes the multiplicative inverse of a matrix.

The method raises a LinAlgError exception if the supplied matrix is not square or the inversion fails.

As shown in the code sample, the supplied matrix doesn't have a determinant of 0, so no LinAlgError is raised.

The numpy.linalg.det() method computes the determinant of an array.

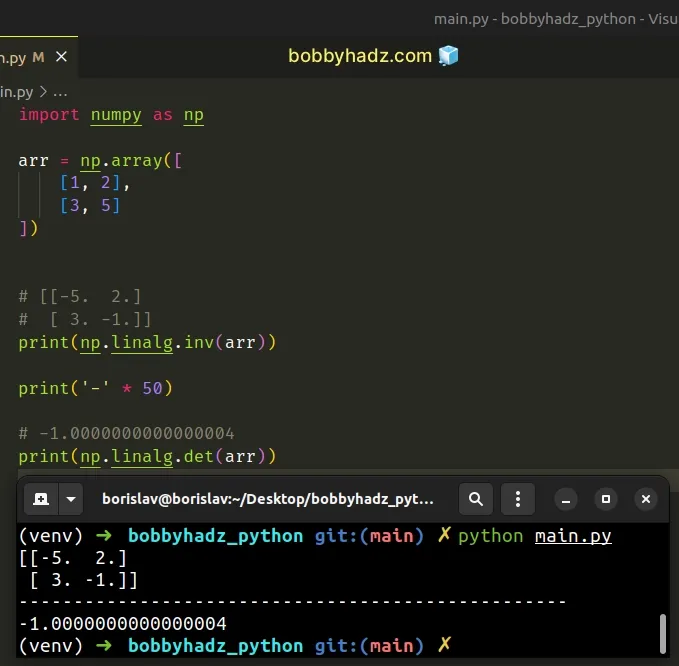
Here is another example.

main.py

Copied!
import numpy as np

arr = np.array([
    [1, 2],
    [3, 5]
])


# [[-5.  2.]
#  [ 3. -1.]]
print(np.linalg.inv(arr))

print('-' * 50)

# -1.0000000000000004
print(np.linalg.det(arr))

another example of invertible matrix

# Make sure you aren't multiplying a 1D vector by its transpose

If you multiply a 1D vector by its transpose, you create a singular matrix that has a determinant of 0 and cannot be inverted.

main.py

Copied!
import numpy as np

arr = np.array([
    1, 2,
    3, 4,
])

# 👇️ [[ 1  2  3  4]
#  [ 2  4  6  8]
#  [ 3  6  9 12]
#  [ 4  8 12 16]]
print(np.transpose(arr[np.newaxis]) * arr)

print('-' * 50)

# 0.0
print(np.linalg.det(np.transpose(arr[np.newaxis]) * arr))

print('-' * 50)

# ⛔️ numpy.linalg.LinAlgError: Singular matrix
print(np.linalg.inv(np.transpose(arr[np.newaxis]) * arr))

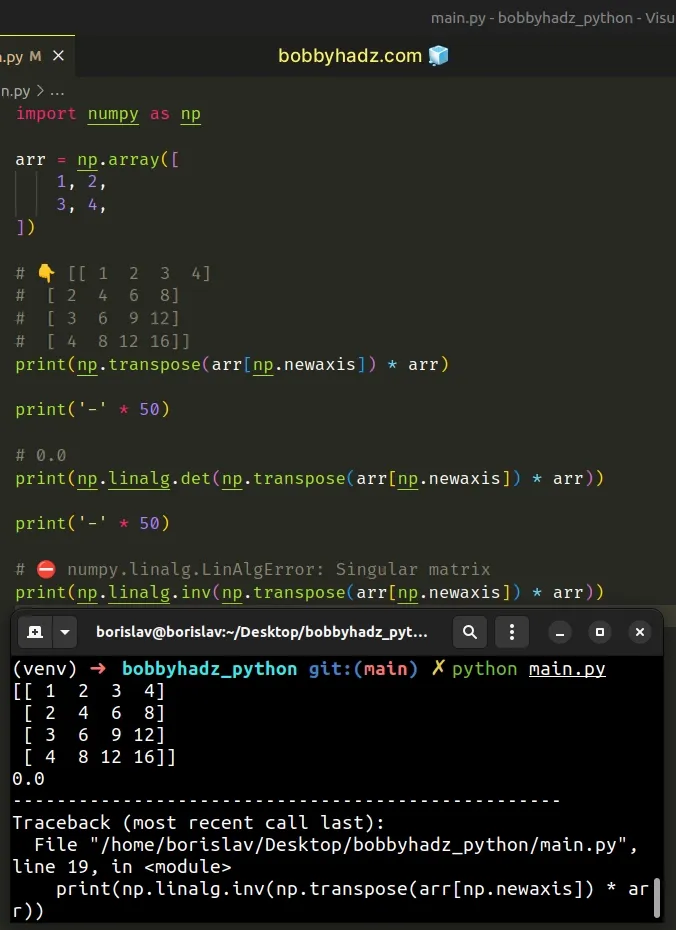
creating singular matrix by mistake by using transpose

The code for this article is available on GitHub

Notice that when you multiply a 1D vector by its transpose, each row is a linear combination of the first row.

The second row is equal to the first row multiplied by 2.

The third row is equal to the first row multiplied by 3, etc.

main.py

Copied!
# 👇️ [[ 1  2  3  4]
#  [ 2  4  6  8]
#  [ 3  6  9 12]
#  [ 4  8 12 16]]
print(np.transpose(arr[np.newaxis]) * arr)

This means that your matrix contains only one independent row and cannot be inverted.

# Use the `numpy.linalg.pinv()` method to solve the error

Even if your matrix cannot be inverted, you can still use the numpy.linalg.pinv() method to compute the Moore-Penrose pseudo-inverse of the matrix.

main.py

Copied!
import numpy as np

arr = np.array([
    [2, 4],
    [2, 4],
])

# [[0.05 0.05]
#  [0.1  0.1 ]]
print(np.linalg.pinv(arr))

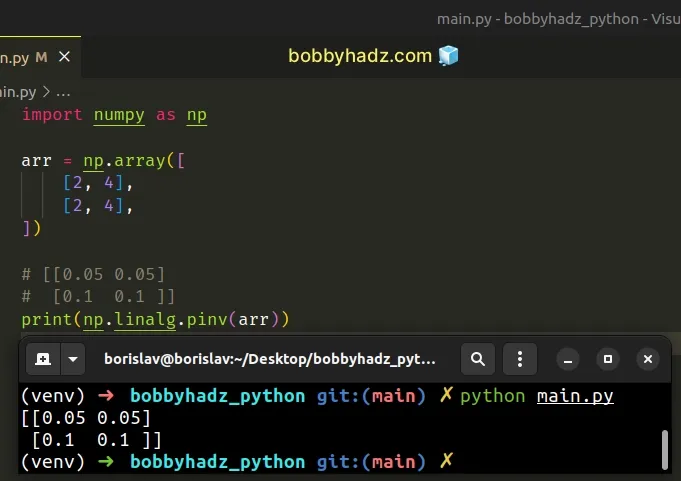
use numpy linalg pinv method to solve the error

The code for this article is available on GitHub

The method calculates the generalized inverse of a matrix using its singular value decomposition (SVD) and includes all large singular values.

The only parameter w passed to the method is the matrix to be pseudo-inverted.

You can read more about using the numpy.linalg.pinv() method in this section of the docs.

If you'd like to read more about singular value decomposition (SVD), check out this Wikipedia page.

# Getting the error when using `numpy.linalg.solve()`

You might also get the error when using the numpy.linalg.solve method.

main.py

Copied!
import numpy as np

a = np.array([
    [2, 4],
    [2, 4],
])


b = np.array([1, 2])

x = np.linalg.solve(a, b)

# ⛔️ numpy.linalg.LinAlgError: Singular matrix
print(x)

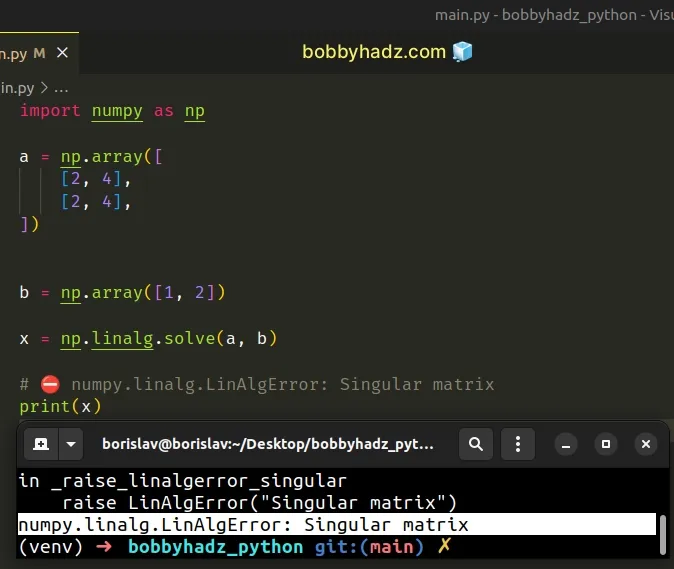
getting the error when using numpy linalg solve

The numpy.linalg.solve method solves a linear matrix equation or system of linear scalar equations.

The two arguments the method takes are:

a - an array-like coefficient matrix.
b - ordinate or "dependent variable" values.

We passed a singular matrix as the first argument to the numpy.linalg.solve() method, so it cannot be inverted.

You wouldn't get the error if the matrix was invertible.

main.py

Copied!
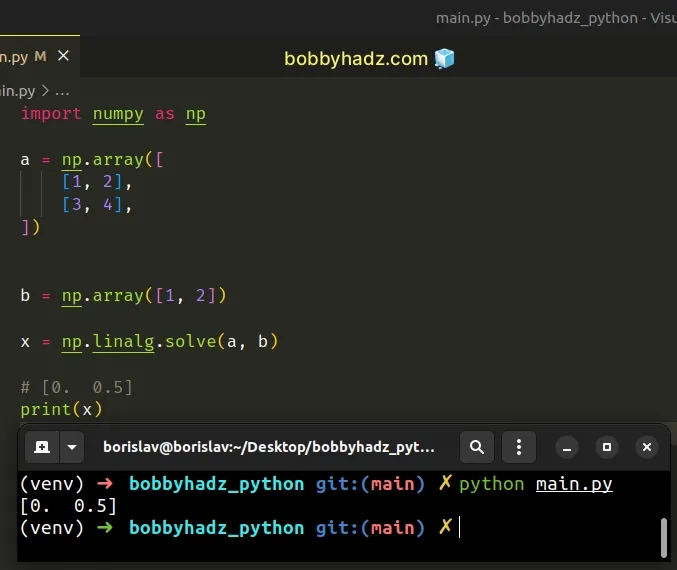
import numpy as np

a = np.array([
    [1, 2],
    [3, 4],
])


b = np.array([1, 2])

x = np.linalg.solve(a, b)

# [0.  0.5]
print(x)

wont get the error if matrix were invertible

The code for this article is available on GitHub

An alternative is to use the numpy.linalg.lstsq method.

main.py

Copied!
import numpy as np

a = np.array([
    [2, 4],
    [2, 4],
])


b = np.array([1, 2])

x = np.linalg.lstsq(a, b, rcond=None)

# (array([0.15, 0.3 ]), array([], dtype=float64), 1, array([6.32455532, 0.        ]))
print(x)

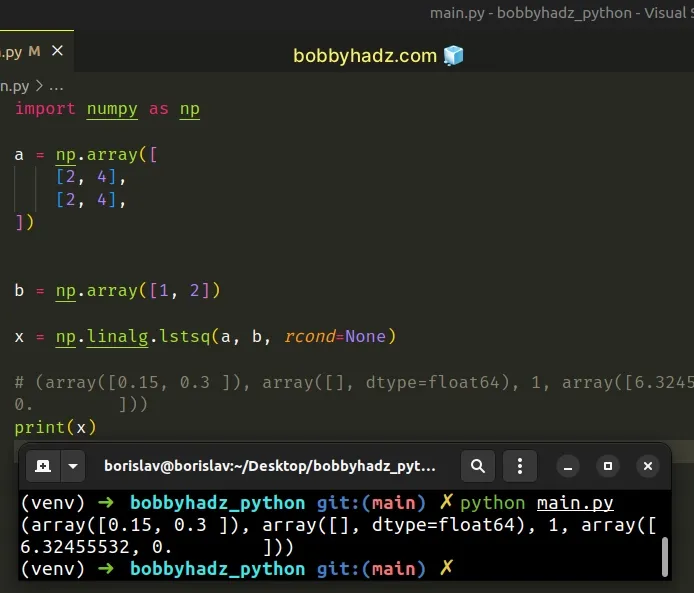
using numpy linalg lstsq method

The numpy.linalg.lstsq method takes a coefficient matrix and an ordinate or "dependent variable" values.

The method returns the least squares solution to a linear matrix equation.

You can read more about the method in this section of the docs.

# Additional Resources

You can learn more about the related topics by checking out the following tutorials:

I wrote a book in which I share everything I know about how to become a better, more efficient programmer.

You can use the search field on my Home Page to filter through all of my articles.

numpy.linalg.LinAlgError: Singular matrix [Solved]

# Table of Contents